hi@zxh
_

RNN 和它的朋友们

Feb 15, 2019 · 13 min · deep learning

对 RNN 系成员的一些总结。

RNN

这是一个三维低等生物眼里的 RNN：

Rolled RNN

这个细胞（绿色的框）相当于 Keras 中一层 RNN 的隐藏层，一个隐藏层可能有多个神经元。它在 tt 时刻的状态（隐状态）叫做 hth_t，是一个向量，向量维数与这个隐藏层的神经元数量相等，每个神经元的值都是一个标量。

这是一个四维高等生物眼里的 RNN（按时间步展开）：

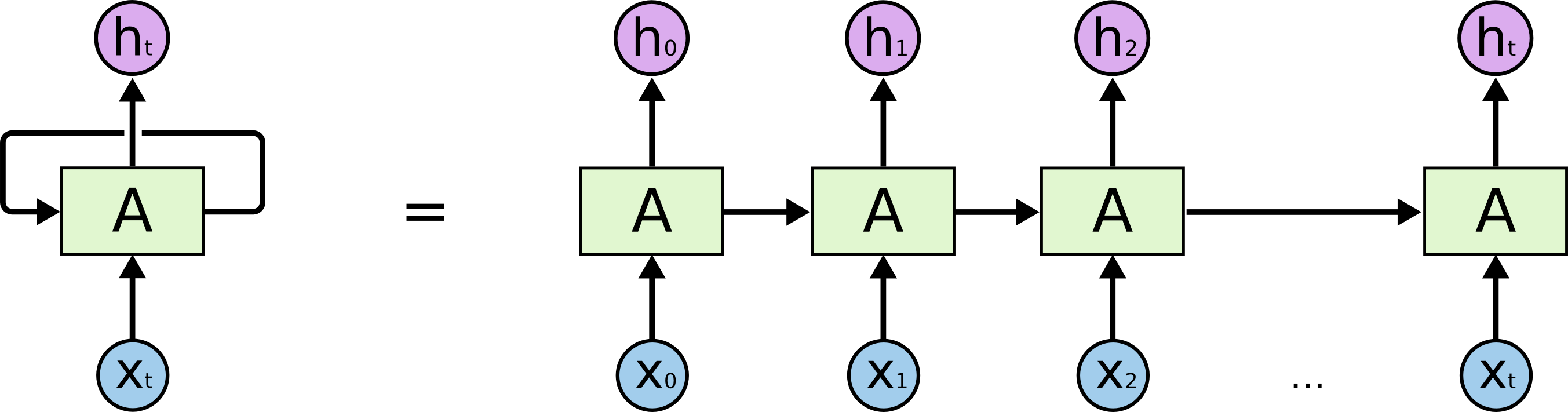
Unrolled RNN

如果画得详细一点：

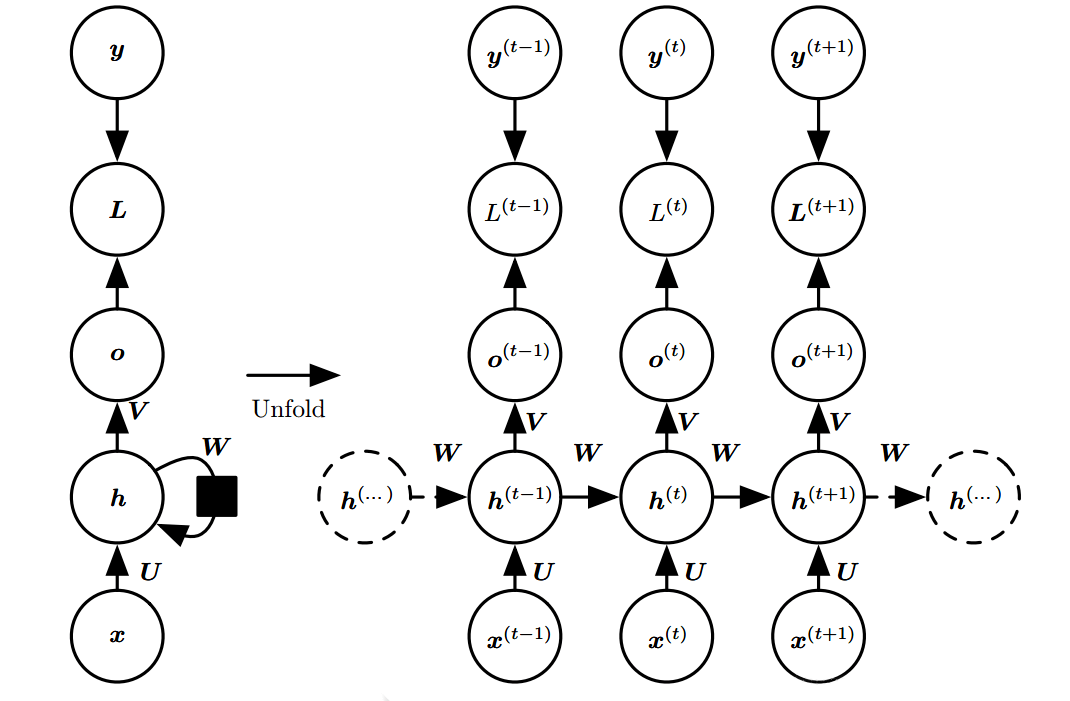
Unrolled RNN's Details

其中：

  • xtx_t：tt 时刻的输入向量；
  • hth_t：tt 时刻的隐状态；
  • oto_t：tt 时刻的输出（只由 hth_t 决定）；
  • LtL_t：tt 时刻的损失函数，最终的损失函数是 ∑tLt\sum_t L_t；
  • yty_t：tt 时刻的真实结果（ground truth）；
  • Wx,Wh,WoW^x, W^h, W^o：权重矩阵，要学习的参数，在所有时间步中都是共享的；

上一个时间步的隐状态 ht−1h_{t-1} 会在 tt 时刻乘一个权重矩阵 WhW^h 然后重新输入细胞，也就是 hth_t 同时依赖于 xtx_t 和 ht−1h_{t-1}。

前向传播

符号说明：

  • f(⋅),g(⋅)f(\cdot), g(\cdot)：激活函数；
  • bb：偏置向量（bias）；
  • y^t\hat{y}_t：模型在 tt 时刻的最终输出；

公式：

ht=f(Wxxt+Whht−1+bh)h_t = f (W^x x_t + W^h h_{t-1} + b_h) ot=Woht+boo_t = W^o h_t + b_o y^t=g(ot)\hat{y}_t = g(o_t)

损失函数 LtL_t 的作用就是量化模型在当前位置的损失，即 y^t\hat{y}_t 和 yty_t 的差距。

反向传播

整体损失函数：

L=∑tnLtL = \sum_t^n L_t

有参数 Wx,Wo,Wh,bo,bhW^x, W^o, W^h, b_o, b_h，先对它们随机初始化，然后在每个迭代周期对各参数求梯度，并按梯度的方向更新这些参数以使 LL 最小化：

Wt+1=Wt−r⋅∂L∂W∣W:Wt,r>0W_{t+1} = W_t - r \cdot \frac{\partial L}{\partial W} \mid_{W:W_t}, r > 0

其中 rr 是学习率，∂L∂W\frac{\partial L}{\partial W} 是损失函数在 W=WtW=W_t 位置的偏导数，即梯度。

Wo,boW^o, b_o 没有长期依赖，所以偏导好求一些：

∂L∂Wo=∑t=1n∂Lt∂Wo=∑t=1n(y^t−yt)(ht)T(=∑t=1n∂Lt∂ot⋅∂ot∂Wo)\frac{\partial L}{\partial W^o} = \sum_{t=1}^n \frac{\partial L_t}{\partial W^o} = \sum_{t=1}^n (\hat{y}_t - y_t)(h_t)^T (= \sum_{t=1}^n \frac{\partial L_t}{\partial o_t} \cdot \frac{\partial o_t}{\partial W^o}) ∂L∂bo=∑t=1n∂Lt∂bo=∑t=1ny^t−yt\frac{\partial L}{\partial b_o} = \sum_{t=1}^n \frac{\partial L_t}{\partial b^o} = \sum_{t=1}^n \hat{y}_t - y_t

而正向传播中，hth_t 对 ht+1h_{t+1} 还有贡献，所以反向传播计算 Wx,WhW_x, W_h 在 tt 时刻的梯度时，还需要考虑 t+1t+1 时刻的梯度（全导数）。

先求 tt 时刻隐状态的梯度：

  • 当 t<nt < n 时，需要从 t+1t+1 时刻递推到 tt 时刻隐状态的梯度：

    ∂L∂ht=(∂ot∂ht)T∂L∂ot+(∂ht+1∂ht)T∂L∂ht+1\frac{\partial L}{\partial h_t} = (\frac{\partial o_t}{\partial h_t})^T \frac{\partial L}{\partial o_t} + (\frac{\partial h_{t+1}}{\partial h_t})^T \frac{\partial L}{\partial h_{t+1}} =(Wo)T(y^t−yt)+(∂ht+1∂zt+1∂zt+1∂ht)T∂L∂ht+1= (W^o)^T(\hat{y}_t - y_t) + (\frac{\partial h_{t+1}}{\partial z_{t+1}} \frac{\partial z_{t+1}}{\partial h_t})^T \frac{\partial L}{\partial h_{t+1}} =(Wo)T(y^t−yt)+(diag(1−ht+1)2Wh)T∂L∂ht+1= (W^o)^T(\hat{y}_t - y_t) + (\text{diag} (1 - h_{t+1})^2 W^h)^T \frac{\partial L}{\partial h_{t+1}} =(Wo)T(y^t−yt)+(Wh)Tdiag(1−ht+1)2∂L∂ht+1= (W^o)^T(\hat{y}_t - y_t) + (W^h)^T \text{diag} (1 - h_{t+1})^2 \frac{\partial L}{\partial h_{t+1}}

  • 当 t=nt = n 时，因为已经是最后一个时刻了，所以：

    ∂L∂hn=(∂on∂hn)T∂L∂on=(Wo)T(y^n−yn)\frac{\partial L}{\partial h_n} = (\frac{\partial o_n}{\partial h_n})^T \frac{\partial L}{\partial o_n} = (W^o)^T(\hat{y}_n - y_n)

然后 Wh,Wx,boW^h, W^x, b_o 的梯度为：

∂L∂Wh=∑t=1ndiag(1−ht2)∂L∂htht−1T\frac{\partial L}{\partial W_h} = \sum_{t=1}^n \text{diag} (1-h_t^2) \frac{\partial L}{\partial h_t} h_{t-1}^T ∂L∂Wx=∑t=1ndiag(1−ht2)∂L∂htxtT\frac{\partial L}{\partial W_x} = \sum_{t=1}^n \text{diag} (1-h_t^2) \frac{\partial L}{\partial h_t} x_t^T ∂L∂bo=∑t=1ndiag(1−ht2)∂L∂ht\frac{\partial L}{\partial b_o} = \sum_{t=1}^n \text{diag} (1-h_t^2) \frac{\partial L}{\partial h_t}

梯度消失和爆炸

如果直接把 WhW^h 在 tt 时刻的偏导式展开：

∂Lt∂Wh=∂Lt∂ot∂ot∂ht∂ht∂Wh+∂Lt∂ot∂ot∂ht∂ht∂ht−1∂ht−1∂Wh+...+∂Lt∂ot∂ot∂ht∂ht∂ht−1∂ht−1∂ht−2...∂h2∂h1∂h1∂Wh=\frac{\partial L_t}{\partial W^h} = \frac{\partial L_t}{\partial o_t} \frac{\partial o_t}{\partial h_t} \frac{\partial h_t}{\partial W^h} + \frac{\partial L_t}{\partial o_t} \frac{\partial o_t}{\partial h_t} \frac{\partial h_t}{\partial h_{t-1}} \frac{\partial h_{t-1}}{\partial W^h} + ... + \frac{\partial L_t}{\partial o_t} \frac{\partial o_t}{\partial h_t} \frac{\partial h_t}{\partial h_{t-1}} \frac{\partial h_{t-1}}{\partial h_{t-2}} ... \frac{\partial h_2}{\partial h_1} \frac{\partial h_1}{\partial W^h} = ∑k=0t∂Lt∂ot∂ot∂ht(∏j=k+1t∂hj∂hj−1)∂hk∂Wh\sum_{k=0}^t \frac{\partial L_t}{\partial o_t} \frac{\partial o_t}{\partial h_t} (\prod_{j=k+1}^t \frac{\partial h_j}{\partial h_{j-1}}) \frac{\partial h_k}{\partial W^h}

同理，WxW^x 在 tt 时刻的偏导式展开为：

∂Lt∂Wx=∑k=0t∂Lt∂ot∂ot∂ht(∏j=k+1t∂hj∂hj−1)∂hk∂Wx\frac{\partial L_t}{\partial W^x} = \sum_{k=0}^t \frac{\partial L_t}{\partial o_t} \frac{\partial o_t}{\partial h_t} (\prod_{j=k+1}^t \frac{\partial h_j}{\partial h_{j-1}}) \frac{\partial h_k}{\partial W^x}

hh 通过激活函数得到，假设激活函数为 tanh：

hj=tanh(WxWj+Whhj−1+bh)h_j = \text{tanh} (W^x W_j + W^h h_{j-1} + b_h) ∏j=k+1t∂hj∂hj−1=∏j=k+1t∂hj∂hj−1tanh′Wh\prod_{j=k+1}^t \frac{\partial h_j}{\partial h_{j-1}} = \prod_{j=k+1}^t \frac{\partial h_j}{\partial h_{j-1}} \text{tanh}' W^h

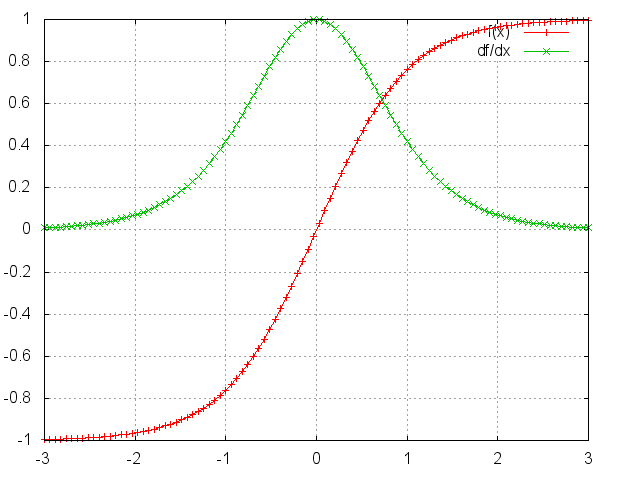
tanh 函数的函数图像和导数图像为：

tanh function

假设激活函数为 sigmoid：

∏j=k+1t∂hj∂hj−1=∏j=k+1t∂hj∂hj−1σ′Wh\prod_{j=k+1}^t \frac{\partial h_j}{\partial h_{j-1}} = \prod_{j=k+1}^t \frac{\partial h_j}{\partial h_{j-1}} \sigma' W^h

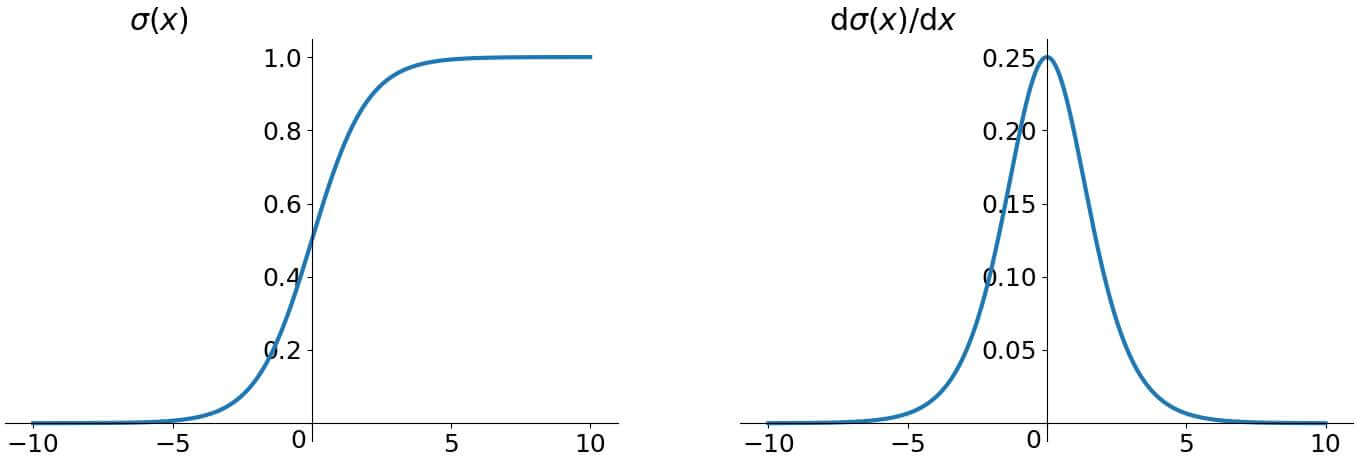
sigmoid 函数的函数图像和导数图像为：

sigmoid function

梯度消失：

可以看到，这俩函数的导数范围都不会超过 1，如果 WhW^h 的初始化值也在 [0,1][0, 1] 之间，那么就是一堆 [0,1][0, 1] 之间的小数在连乘，乘到最后就会导致梯度越来越接近于 0，造成梯度消失。

在 DNN 中，某一层的梯度消失就意味着那一层的参数再也不更新，那一层的隐层就变成了单纯的映射层。

而 RNN 中，梯度是累加的，就算较远时刻的梯度趋近于 0，累加后的整体梯度依然不会为 0，整体梯度是不会消失的。但这会造成 RNN 被近距离梯度主导，只能利用的有限的历史数据，难以学到远距离的依赖关系。

但相比 sigmoid，tanh 函数的梯度还是更大一点，所以收敛速度要快一些，且引起梯度消失更慢。

而解决梯度消失可以靠换激活函数（ReLU、LeakyReLU、ELU 等）或改传播结构（LSTM、Batch Normalization、ResNet 残差结构）。

如，ReLU 激活函数的函数图像和导数图像为：

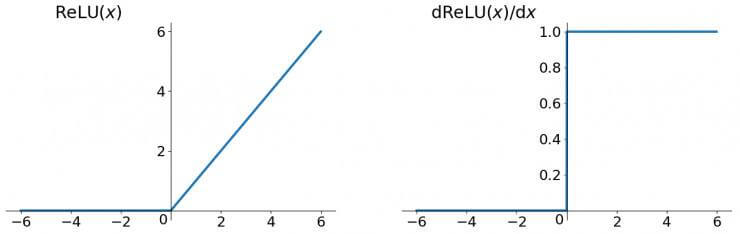
relu function

因为 yy 轴右侧导数恒为 1，所以避免了梯度消失的问题。但恒为 1 的导数容易导致梯度爆炸，所以需要一些调参技巧，比如给梯度设定合适的阈值，如果大于这个阈值，就按这个阈值进行更新。

梯度爆炸：

而如果 WhW^h 的初始化值非常大，那连乘起来就会梯度爆炸。梯度爆炸意味着可能因为过大的优化幅度而跨过最优解，导致前面的学习过程白费。

LSTM

Long Short-Term Memory. Sepp Hochreiter and Jürgen Schmidhuber. Neural Computation 1997. [Paper]

一般来说应该放一张这样的图：

LSTM

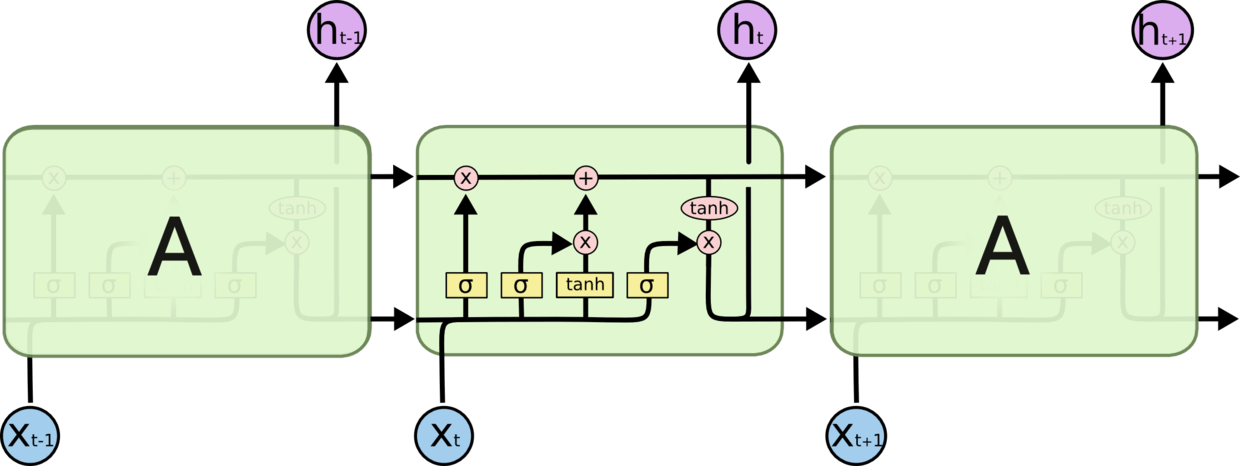
同样，这个细胞相当于 Keras 中一层 LSTM 的隐藏层，隐藏层里有四个前馈网络层。图里的 4 个黄色框每个都是一个前馈网络层，它们的激活函数分别为 sigmoid（1，2，4）和 tanh（3）。

Hidden Units（Keras 的 units）就是每个前馈网络层的神经元个数。

另一种画法（论文 Show and Tell），虽然它似乎把 output gate oo 写成了 output gate ff（…）：

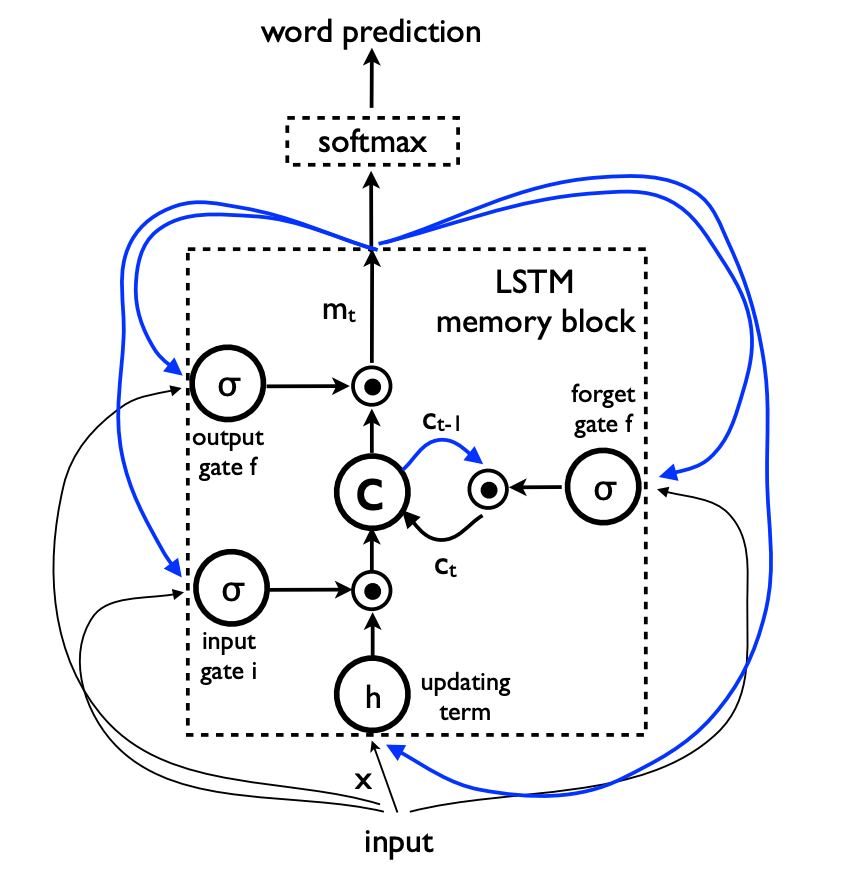
Also a LSTM

LSTM 的核心是一个由 3 个门控制的记忆细胞 cc。t−1t-1 时的隐状态 ht−1h_{t-1} 会被用于当前细胞状态的损失计算，和下一细胞状态（tt 时）的隐状态 hth_t 的计算，所以 ht−1h_{t-1} 会在 tt 时经过这 3 个门重新进入细胞。

前向传播

传播流程：

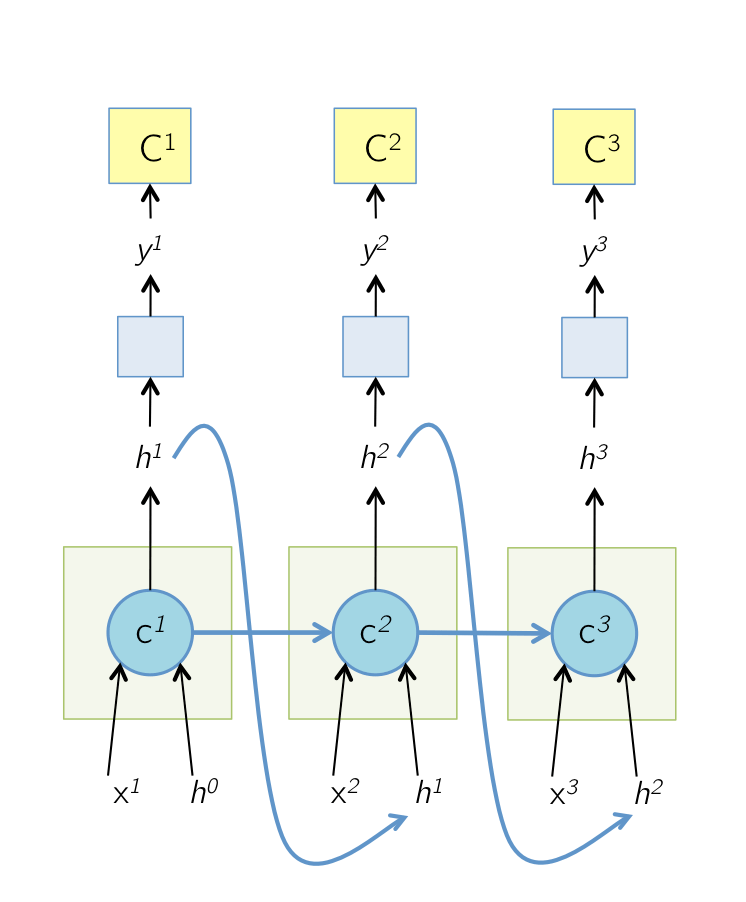
LSTM Forward

后面公式中的符号说明：

  • σ(⋅)\sigma(\cdot)：sigmoid 激活函数，会把矩阵转换为一个介于 0 和 1 之间的值作为门控信号，0 表示完全遗忘，1 表示完全接受；
  • tanh(⋅)\text{tanh}(\cdot)：tanh 激活函数，会把矩阵转换为一个介于 -1 和 1 之间的值；
  • ⊙\odot：哈达玛积（Hadamard Product），即俩矩阵对应元素相乘，所以要求俩矩阵同形

遗忘门

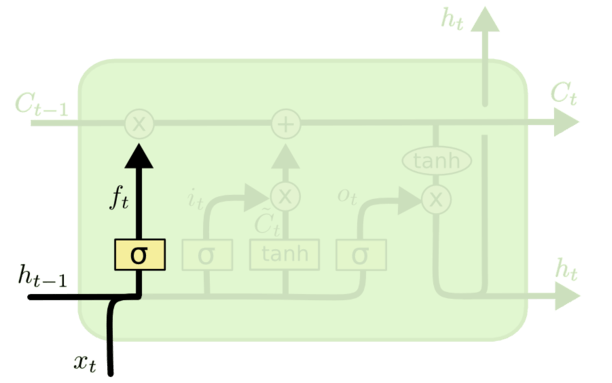
Forget Gate

Forget Gate，对上一个细胞状态传进来的信息进行选择性遗忘。会根据 ht−1h_{t-1} 和 xtx_t 来为上一个细胞状态 ct−1c_{t-1} 计算一个门控信号，计算公式为：

ft=σ(Wfxxt+Wfhht−1+bf)f_t = \sigma (W_{fx} x_t + W_{fh} h_{t-1} + b_f)

然后把 ftf_t 跟 ct−1c_{t-1} 相乘，就是最终从上一个状态输入的内容：

ft⊙ct−1f_t \odot c_{t-1}

输入门

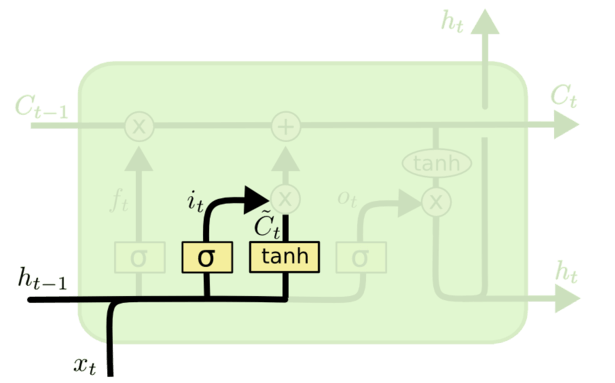
Input Gate

Input Gate，对现阶段输入 xtx_t 进行选择性记忆，更新细胞状态。由两个部分构成：

  • sigmoid 激活函数，计算门控信号，控制要记忆哪些内容：

    it=σ(Wixxt+Wihht−1+bi)i_t = \sigma (W_{ix} x_t + W_{ih} h_{t-1} + b_i)

  • tanh 激活函数，计算现阶段新学到的东西：

    c~t=tanh(Wcxxt+Wchht−1+bc)\tilde{c}_t = \text{tanh}(W_{cx} x_t + W_{ch} h_{t-1} + b_c)

这俩相乘后的结果就是最终被记下来的现阶段新学到的东西，再加上从上一个细胞状态输入的内容就是更新后的细胞状态。所以细胞状态的更新公式为：

ct=ft⊙ct−1+it⊙c~tc_t = f_t \odot c_{t-1} + i_t \odot \tilde{c}_t

输出门

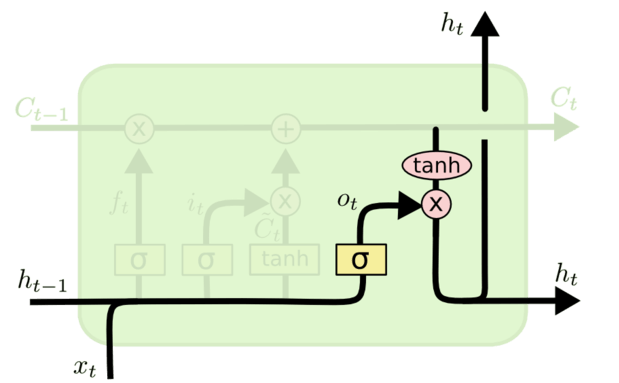
Output Gate

Output Gate，现在细胞状态已经更新了，所以要决定那些状态最终会被输出（隐状态 hth_t）。依然用 sigmoid 激活函数来计算一个门控信号，控制要输出哪些内容：

ot=σ(Woxxt+Wohht−1+bo)o_t = \sigma (W_{ox} x_t + W_{oh} h_{t-1} + b_o)

然后把它跟用 tanh 激活函数放缩过的当前细胞状态 ctc_t 相乘，就是这个阶段最终输出的隐状态：

ht=ot⊙tanh(ct)h_t = o_t \odot \text{tanh}(c_t)

最终输出

最终的输出 yty_t 会由 hth_t 变换得到，常见的做法大概是把 hth_t 扔进 softmax：

yt=softmax(ht)y_t = \text{softmax}(h_t)

反向传播

传播流程：

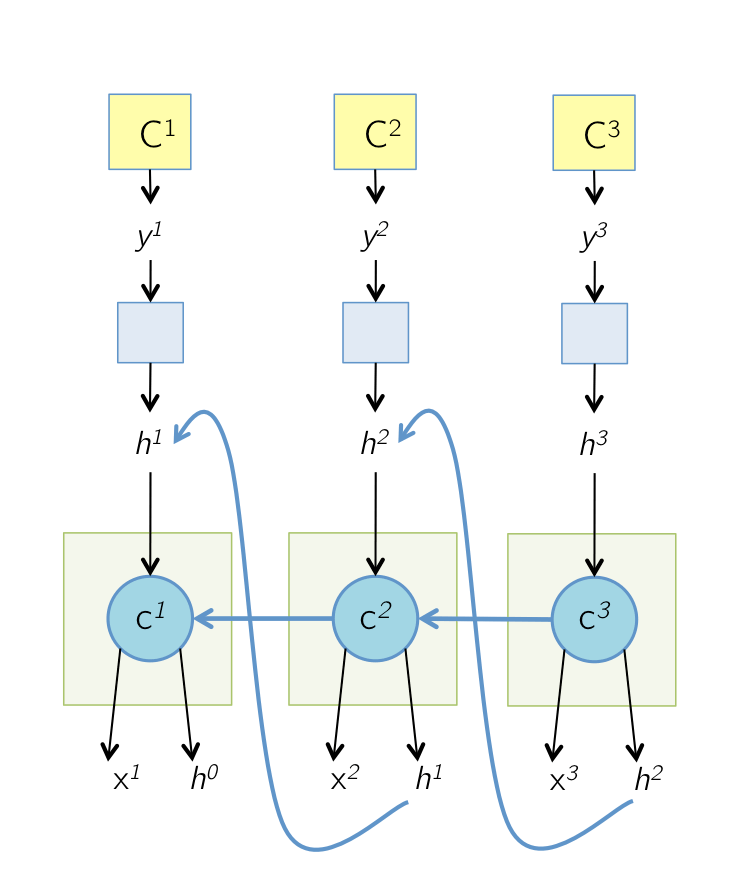
LSTM Backward

公式以后再说，我已经跑偏太多了…

GRU

GRU

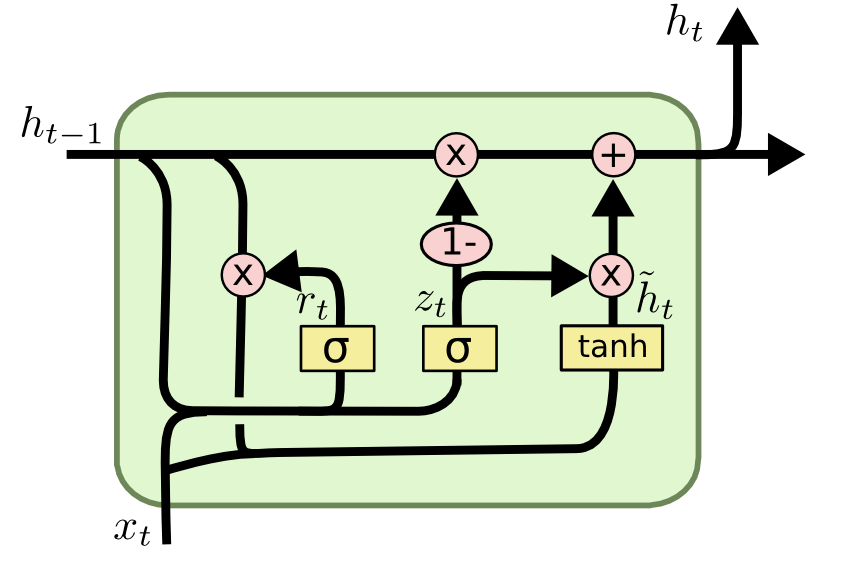
GRU 是 LSTM 的变体。它只有两个门，重置门 rtr_t 和更新门 ztz_t（用一个门达到了遗忘和输入的目的）。它还合并了隐状态和细胞状态。它的模型结构比 LSTM 简单，但同时能达到跟 LSTM 相当的效果。

重置门

Reset Gate，先计算重置门控信号 rtr_t，用于控制要保留上一个时刻的多少信息：

rt=σ(Wrxxt+Wrhht−1+br)r_t = \sigma (W_{rx} x_t + W_{rh} h_{t-1} + b_r)

然后计算当前时刻的候选隐状态（candidate hidden state）：

h^t=tanh(Whxxt+rt⊙(Whhht−1)+bh)\hat{h}_t = \text{tanh} (W_{hx} x_t + r_t \odot (W_{hh} h_{t-1}) + b_h)

相当于 h^t\hat{h}_t 主要包含了当前输入 xtx_t 的信息，然后有选择性的加入上一时刻的信息（ht−1h_{t-1}）。

更新门

Update Gate，先计算更新门控信号 ztz_t，用于控制要从 ht−1h_{t-1} 中遗忘多少信息和要从 h^t\hat{h}_t 中记忆多少信息：

zt=σ(Wzxxt+Wzhht−1+bz)z_t = \sigma (W_{zx} x_t + W_{zh} h_{t-1} + b_z)

然后直接算出当前时刻隐状态 hth_t：

ht=(1−zt)⊙ht−1+zt⊙h^th_t = (1 - z_t) \odot h_{t-1} + z_t \odot \hat{h}_t

可以理解为 (1−zt)(1 - z_t) 对标 LSTM 中的遗忘门控，ztz_t 对标 LSTM 中的输入门控。

Reference

Edit this page on GitHub Last updated: 3/7/2023, 2:57:21 PM
线性代数笔记 RACF 实验